
Zadanie Dziwna planeta (pla)
Pomóż nam usprawnić bazę zadań!
Dziwna planeta
Limit pamięci: 32 MB
Pewnego razu gdzieś tam sobie istniała  -wymiarowa przestrzeń. Znajdowała się tam również pewna dziwna planeta. Jedną z jej przedziwnych cech był jej kształt -
-wymiarowa przestrzeń. Znajdowała się tam również pewna dziwna planeta. Jedną z jej przedziwnych cech był jej kształt -  -wymiarowy hipersześcian o jednostkowej długości boku. W każdym wierzchołku planety znajdowało się pewne dziwne miasto.
-wymiarowy hipersześcian o jednostkowej długości boku. W każdym wierzchołku planety znajdowało się pewne dziwne miasto.
Terytorium tej planety zostało podzielone między trzy wrogie królestwa. Jednak kilka miast ogłosiło swoją niezależność - nazwijmy je neutralnymi: 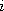 -te miasto jest niezależne, jeśli
-te miasto jest niezależne, jeśli 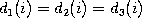 , gdzie
, gdzie 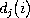 oznacza odległość między
oznacza odległość między 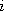 -tym miastem oraz stolicą
-tym miastem oraz stolicą 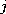 -tego królestwa. Wszystkie odległości liczone są przy pomocy metryki miejskiej.
-tego królestwa. Wszystkie odległości liczone są przy pomocy metryki miejskiej.
Twoim zadaniem jest obliczenie liczby neutralnych miast. Ze względu na to że wynik może być duży, wystarczy wypisać go modulo 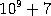 .
.
Wejście
Wejście zawiera trzy linie. W każdej linii znajdują się współrzędne stolicy kolejnego królestwa w postaci liczby binarnej długosci  (
(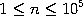 ).
).
Wyjście
W pierwszym i jedynym wierszu wyjścia powinna się znaleźć jedna liczba całkowita równa liczbie neutralnych miast modulo 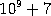 .
.
Przykład
Dla danych wejściowych:
01 01 10
poprawną odpowiedzią jest:
2
Autor zadania: Adrian Jaskółka (zapożyczenie).
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English